4.1 Stress At A Point - 2D

4.1.1 Stresses on Rotated Planes

Suppose that we know the stress state of the soil on a particular plane, and we wish to determine the stress state on a different, rotated plane. This problem is equivalent to a transformation of the coordinate system. The components of the Cauchy stress tensor in the rotated coordinate space, \(\hat{\sigma}_{ij}\), can be determined from the stress components in the reference state, \(\hat{\sigma}_{ij}\), using the rotation matrix \(a\) with components \(a_{ij}\). Note that in soil mechanics, we often represent the shear stress components (i.e., the off-diagonal elements of the stress tensor) as \(\tau_{ij}\) instead of \(\sigma_{ij}\). Furthermore, the prime in \(\sigma'\) usually denotes effective stress, but is used here to denote stresses in a rotated coordinate system.

$$\hat{\sigma} = a \sigma a^T$$ In soil mechanics, we often simplify three-dimensional stress conditions to two dimensions. The Mohr Circle is a very common tool used to interpret soil stress states, and it is inherently a two-dimensional representation of stresses. We should therefore consider rotation of stresses in two dimensions. Figure 4.1.1 defines the terms of the rotation tensor, \(a_{ij}\).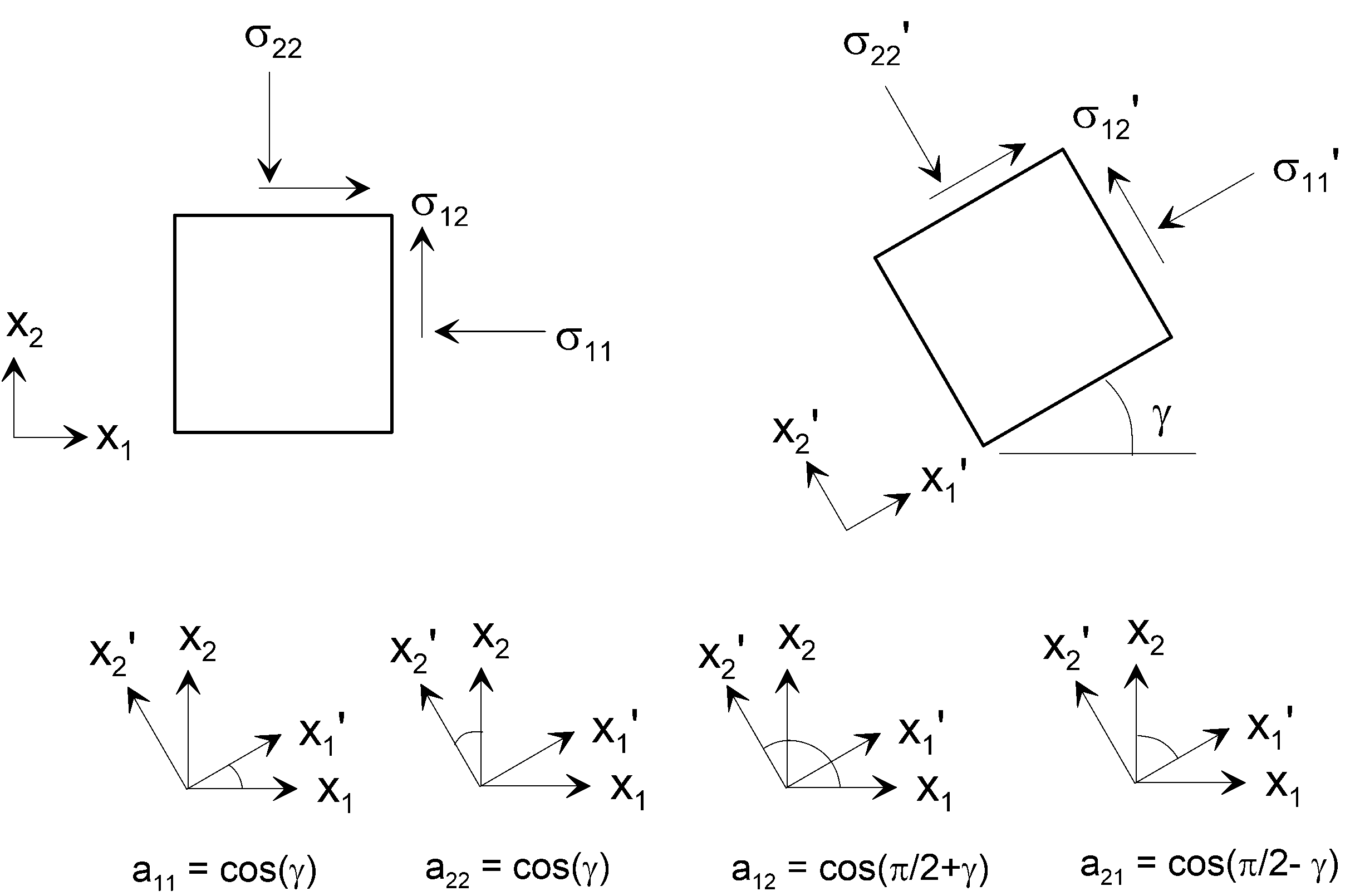

Figure 4.1.1. Two dimensional coordinate system rotation (note rotation is about the \(x_3\) axis by angle \(\gamma\)).

The rotated stress state can therefore be defined as follows: \[\left[ \begin{matrix} \sigma _{11}^{'} & \hat{\sigma}_{12} \\ \sigma _{21}^{'} & \hat{\sigma}_{22} \\ \end{matrix} \right]=\left[ \begin{matrix} \cos (\gamma ) & -\sin (\gamma ) \\ \sin (\gamma ) & \cos (\gamma ) \\ \end{matrix} \right]\left[ \begin{matrix} {{\sigma }_{11}} & {{\sigma }_{12}} \\ {{\sigma }_{21}} & {{\sigma }_{22}} \\ \end{matrix} \right]\left[ \begin{matrix} \cos (\gamma ) & \sin (\gamma ) \\ -\sin (\gamma ) & \cos (\gamma ) \\ \end{matrix} \right]\]

Expanding out the matrix algebra results in the following expressions for the rotated stresses: \[\begin{align} & \hat{\sigma}_{11}={{\sigma }_{11}}-{{\sigma }_{12}}\sin (2\gamma )-{{\sin }^{2}}(\gamma )\left( {{\sigma }_{11}}-{{\sigma }_{22}} \right) \\ & \hat{\sigma}_{22}={{\sigma }_{22}}+{{\sigma }_{12}}\sin (2\gamma )+{{\sin }^{2}}(\gamma )\left( {{\sigma }_{11}}-{{\sigma }_{22}} \right) \\ & \hat{\sigma}_{12}={{\sigma }_{12}}\cos (2\gamma )+\frac{\sin (2\gamma )}{2}\left( {{\sigma }_{11}}-{{\sigma }_{22}} \right) \\ \end{align}\]

Try it yourself